弓の重心操作の危険性
1997年7月9日 日本弦楽器製作者協会員
ドイツ・ヴァイオリン製作マイスター 佐々木朗
- 安易な重心操作の危険性
- まず一番最初に、現状において「弓の安易な重心操作」がまかり通っていることに対して、その危険性を警告しなければなりません。
残念ながら、多くの演奏者や技術者は「弓のバランス」というものについて勘違いをしています。すなわち、「弓の重さ」と「静的重心」のみにしか目がいっていないのです。このような考え方のみで弓を取り扱うと、巻線や鉛なによって、弓のバランスを安直に変えてしまいがちなのです。
実際の弓は、天秤のようにいつも同じ位置でぶら下がっているものではありません。その瞬間瞬間で、弓が弦に置かれる位置は変化します。また、それだけではなく、弓は上下にも運動します。このような非常に複雑な運動をする弓のバランスを、単純な「質量と、静的な重心」のみで考えるにはあまりにも無理があるのです。
- 重心の求め方
- 弓のバランスを考える上で、「重心」の理論的計算方法は避けて通ることはできません。以下に、巻線によって起こる弓の重心変化の求め方を書きます。
重心はそれぞれの質点系について、その「質量×距離」を求め、それを足し合わせ、そして全体の質量で割ったものとして求めることができます。これを物理学的に書くと、次のようになるのです。
∫rσdr
重心の座標 Ｇ＝───────
M＋m
Nσ（b２ -a２）
＝ ───────
M＋m
- M：巻線なしの弓の重さ
m：巻線の重さ
σ：１mm幅巻いた時の巻線の質量
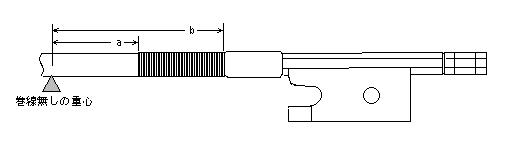
a：最初の重心位置から巻きはじめの点までの距離
b：最初の重心位置から巻き終わりの点までの距離
ちなみに上記の数式中の「m」と「σ」は次のようにして求めることができます。
m＝（弓の直径＋巻線の直径）×3.14×線密度×巻いた区間の長さ / 巻線の直径
σ＝（弓の直径＋巻線の直径）×3.14×線密度 / 巻線の直径
- 巻線の「直径」と、「線密度」のデータ
-
| 巻線の種類 |
直径 |
線密度 |
| 洋銀線 |
φ 0.250mm |
4.27×10-4g/mm |
| 銀線 （太） |
φ 0.300mm |
7.41×10-4g/mm |
| 〃 （中） |
φ 0.250mm |
4.41×10-4g/mm |
| 銀糸線 |
φ 0.500mm |
3.89×10-4g/mm |
| 〃 |
φ 0.375mm |
2.36×10-4g/mm |
| 金線18K（太） |
φ 0.300mm |
1.01×10-3g/mm (Au75% Ag15% Cu10%) |
| 〃 （中） |
φ 0.250mm |
6.04×10-4g/mm |
| 金線14K（太） |
φ 0.300mm |
8.53×10-4g/mm (Au59% Ag12% Cu25%) |
| 〃 （中） |
φ 0.250mm |
5.08×10-4g/mm |
| 鯨のひげ |
|
1.05×10-3g/mm (幅1.6mm 厚み0.6mm) |
余談になりますが、上記の「線密度」の大きさは、直接、重心移動の割合に結びつくものではありません。なぜならば、例え線密度の大きい巻線でも、その直径が大きければ（太ければ）、太いぶんだけ巻き付ける長さが短くてもすむからです。
このような意味からも、「重心の計算」無しに、安易な感覚でバランス操作を行う事は危険なのです。
- 巻線の種類と、重心移動
- さて、これまでに説明してきました重心の計算方法を利用すると、実際に巻線を巻くこと無しに、重心の変化を予測できます。下記に、６種類の巻線における重心を計算し、標準銀線（φ
0.25mm）との差を比較してみました。
| 巻線の種類 |
直径 |
巻線区間は50mm |
| 銀線（太） |
φ 0.300mm |
+2.0mm +39% |
| 〃（基準） |
φ 0.250mm |
- - |
| 銀糸線 〃 |
φ 0.375mm |
-3.2mm -62% |
| 金線14K（太) |
φ 0.300mm |
+3.0mm +59% |
| 〃 （中) |
φ 0.250mm |
+0.8mm +16% |
| 鯨のひげ |
− |
-3.1mm -61% |
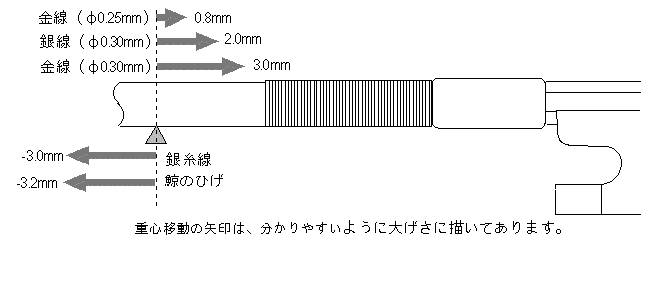標準的な巻線は0.25mm太の銀線です。一方、0.30mmの銀線は、一見したところでは0.25mmと比べて、大した違いはないと感じるかもしれません。しかし、その重心移動量は、見かけ以上に大きなものなのです。まして、大目に（長く）巻線を巻いたり、またはより密度の大きな「金線」を使用した場合には、重心の移動量は、その弓の持つ特徴を殺してしまうでしょう。 銀糸線と鯨のひげを巻いた場合には、弓の重心は弓の先端側に移動します。すなわち、巻線の影響が少ないのです。銘弓などは弓の竿自信が持つバランス性能を壊さないためにも、このように影響力の少ない巻線が使われることが多いです*1。
*1実際には、鯨のひげや銀糸線は、金属巻線よりも長めの区間巻く場合が多いので、重心の移動距離はここまで大きく「マイナス」になるわけではありません。
- 銀チップ、重りによる重心移動
- 巻線による操作の他に、チップを銀チップに交換したり、または弓先端に鉛を入れる操作も、よく目にします。このような操作による効果も、先の計算方法の応用にて考える事ができるのです。
- チップを象牙から銀に換えた場合
- 象牙（牛骨）チップ 0.25g
銀チップ 0.65g （厚み0.5mm ）
計算の結果、象牙チップを銀チップに換えることによってＧ＝+3.7mmという結果がでました。チップの位置は重心点より大きく離れているために、ほんの0.4gの差でも顕著な差として現われたのです。この計算結果からも、チップの重さは0.1g単位で、神経質に決定しなければなりません。まして、チップの中に鉛を詰めるということは、別次元の話となってしまうのです。 また、巻線、チップ交換、重りによる操作は、単に重心の極端な移動だけではないのです。どちらかといえば、これから述べる「運動性能」の変化の方がより悪影響があるのです。
重りと、運動性能（慣性モーメント）の関係
一番最初でも述べましたように、弓は「静的」なものではありません。「動的」なのです。従って、天秤のように静止した状態での重心と重さは、弓の大切な要素の中の一部でしかないのです。
ここでは弓を動かす上で大切な要素となる「バランス」と「慣性モーメント」について、簡単な仮想実験を行ってみましょう。
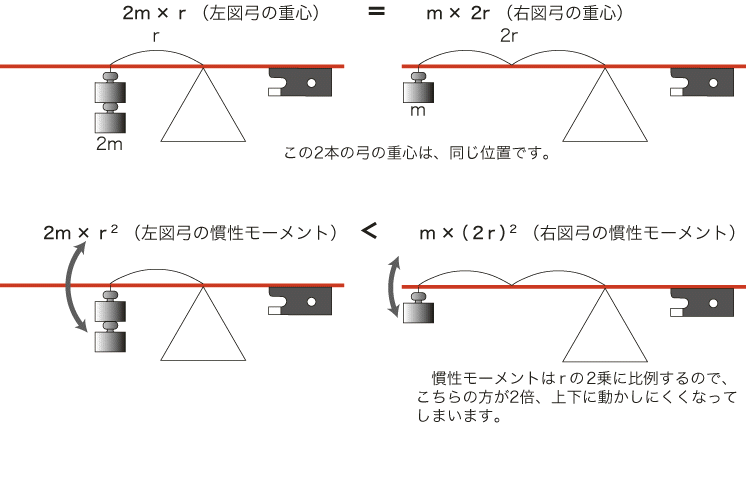
図の上段が弓の静的バランスを現しています。一般的に演奏者や技術者の言う「バランス」とは、この「静的バランス」、すなわち「重心位置」の事を指しています。しかし、図上段の２本の弓のように重心位置は全く同じ弓でも、その慣性モーメントは全く異なります（図下段）。
この仮想実験での弓は、実際の弓の運動とは異なっています。しかしこのような単純な比較だけにおいても、静的状態で同じバランスであった弓でも、回転運動においては特徴が異なるということを理解していただけたと思います。
- 弓の「バランス」の本来の意味とは
- これまでに、安易なバランス操作は弓に悪影響があるということを述べてきました。それでは、本来の意味での「弓のバランス」とはいったいどのようなことを指しているのでしょうか？
弓のバランスとは、これまでにも説明してきましたように、非常に複雑な要素を持っています。すなわち、様々な弓の運動、状態におけるバランスなのです。従って、弓の一部分に小細工をしても、弓の複雑な運動における、ほんの一面でしか効果がないのです。逆に言えば、その他の面においては、不自然になる場合が多いのです。
真の意味でのバランスとは、弓の竿自体が持っています。従って、バランスの良くない竿をどんなに小細工しても、決して本来の意味での「良いバランス」にはなりません。これは仕方のないことです。問題なのは、良質な弓に小細工をすることによって、その弓の持つ「自然な、良いバランス」を殺してしまうことです。
弓の本来の調整とは、弓の竿が持つバランス性能を引き出してあげることなのです。